What You Should Know
What You Will Learn
- How to classify intervals
- What enharmonic intervals are
- What compound intervals are
- How to invert intervals
How to Identify Intervals
What is an Interval?
An interval is the distance in pitch between two notes. Intervals are named according to the number of notes (letter names) and half-steps between the two notes.
Melodic and Harmonic Intervals
Intervals can be either melodic or harmonic. Melodic intervals occur when the notes involved are played separately, as in a melody. Harmonic intervals are when the notes are played at the same time.
Classifying Intervals
Interval Names
Interval names consist of two parts:
- a number for the size of the interval (unison, second, third, fourth, fifth, sixth, seventh, or octave)
- a prefix for the quality of the interval (major, minor, perfect, diminished, or augmented)
Here are a few examples of possible interval names using the conventions above:
- minor third
- perfect fourth
- augmented sixth
The interval is almost always determined by starting on the lower pitch. All examples in this lesson work this way, but there are situations where you may need to determine an interval below a pitch. For example, you may need to transpose music down by a certain interval to play it in a different key.
Interval Number
The number or size of an interval can be determined by counting the number of letter names between the two pitches. You should begin counting with the number one on the lower pitch. Try this with the example below:
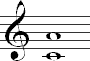
The interval from C to A includes six pitches (C, D, E, F, G, A), so it is a sixth. Keep in mind that there are seven letters in the music alphabet from A to G, so if you reach G, you start over with A until you reach the second note in the interval.
The following chart shows the basic interval names and how many letter names are in each:
| Interval name | Number of letters |
|---|---|
| unison | 1 |
| second | 2 |
| third | 3 |
| fourth | 4 |
| fifth | 5 |
| sixth | 6 |
| seventh | 7 |
| octave | 8 |
Note that the unison and octave are usually referred to using these names rather than a numerical value, such as first or eighth.
Here is an example of each of these intervals starting on C:

Interval Quality
The prefix part of an interval name can be determined by counting the number of half-steps between the two pitches. Each of these prefixes will only be used with certain intervals. Major and minor will only be used with seconds, thirds, sixths, and sevenths, while perfect will only be used with unisons, fourths, fifths, and octaves. Augmented and diminished can be used with any interval. The chart below summarizes details about interval quality.
| Interval quality | Description | Used with |
|---|---|---|
| Augmented | One half step larger than either a major or perfect interval | any interval |
| Diminished | One half step smaller than either a minor or perfect interval | any interval |
| Major | One half step larger than a minor interval | seconds, thirds, sixths, and sevenths |
| Minor | One half step smaller than a major interval | seconds, thirds, sixths, and sevenths |
| Perfect | n/a | unisons, fourths, fifths, octaves |
Double Augmented and Diminished Intervals
It is possible to have a doubly augmented or diminished interval, but these occur rarely. A doubly augmented interval will be one half step larger than an augmented interval, while a doubly diminished interval will be one half step smaller than a diminished interval.
Shorthand Notation for Interval Quality
These prefixes are often written in shorthand followed by a number for the numerical value of the interval:
- A for augmented
- d for diminished
- M for major
- m for minor
- P for perfect
Note the capitalization of each prefix. Minor and diminished should be indicated with lower case letters. The other prefixes should be capitalized. The chart below lists common intervals and the shorthand notation for each of them.
| Shorthand | Interval |
|---|---|
| m2 | minor second |
| M2 | major second |
| m3 | minor third |
| M3 | major third |
| P4 | perfect fourth |
| A4 | augmented fourth |
| d5 | diminished fifth |
| P5 | perfect fifth |
| m6 | minor sixth |
| M6 | major sixth |
| m7 | minor seventh |
| M7 | major seventh |
Note that unisons and octaves can also be written in shorthand by using a "1" for a unison and an "8" for an octave. However, unisons and octaves are generally called by these names rather than the shorthand.
Determining the Quality of an Interval
The quality of an interval is determined by the number of half steps between the two notes. The chart below gives the number of half steps in the most common intervals.
| Interval | # of Half Steps |
|---|---|
| unison | 0 |
| minor second | 1 |
| major second | 2 |
| minor third | 3 |
| major third | 4 |
| perfect fourth | 5 |
| augmented fourth | 6 |
| diminished fifth | 6 |
| perfect fifth | 7 |
| minor sixth | 8 |
| major sixth | 9 |
| minor seventh | 10 |
| major seventh | 11 |
| octave | 12 |
Enharmonic Intervals
Enharmonic intervals are intervals that sound the same although they are notated differently. They will have the same number of half-steps, but the number of notes will be different. An example of enharmonic intervals is shown below:

Both of the intervals sound the same and have the same number of half steps (5), but each interval has a different number of notes in terms of the letter names between the bottom and top note. The first interval is a perfect fourth. There are four letter names in this interval (C D E F) and five half steps. The second interval is an augmented third. The interval contains three letter names (C D E) and five steps. Although these intervals sound the same, it is important to distinguish between them by using the correct name. The name of the interval is very important in constructing and analyzing things like chords and scales, so make sure to name each interval correctly.
The Tritone
The tritone is the most common enharmonic interval. Tritone is another name for an augmented fourth. The name 'tritone' comes from the three (tri-) whole tones (tone) in the augmented fourth. Although the diminished fifth technically doesn't contain three whole tones, the word tritone is used to describe it as well, since a diminished fifth and augmented fourth are enharmonic intervals.
The tritone can be written in shorthand as A4 or d5 depending on the notes involved, but "TT" is another shorthand for the tritone that is used frequently.
Interval Inversions
Intervals can be inverted by raising the lower pitch by an octave. The quality and size of the interval always follows a certain pattern when inverted. For example, if a third is inverted it is always a sixth.
Inversions: Size
Table of Inversions by Size
The table below lists the inversion of each interval when inverting according to size.
| Intervals | Inversion |
|---|---|
| Unison | Octave |
| Second | Seventh |
| Third | Sixth |
| Fourth | Fifth |
| Fifth | Fourth |
| Sixth | Third |
| Seventh | Second |
| Octave | Unison |
Examples of Inverting by Size
The following example shows how each of these intervals are inverted using C as the bottom note. The first interval is the original interval. The second interval in each measure is the inversion.

Inversions: Quality
Table of Inversions by Quality
The following table gives the inversion of each quality: augmented, diminished, major, minor, and perfect. Like inversions of size, these inversion are always the same.
| Quality | Inversion |
|---|---|
| Augmented | Diminished |
| Diminished | Augmented |
| Major | Minor |
| Minor | Major |
| Perfect | Perfect |
Sample Inversions by Quality above a C
An example of each quality inversion is shown below.

Simple and Compound Intervals
Simple intervals are an octave or smaller. Compound intervals are intervals that are larger than an octave. Intervals of a ninth, tenth, eleventh, twelfth, and thirteenth are the most common compound intervals. These intervals can have the same qualities as their simple interval counterparts.
Comparing Simple and Compound Intervals
Every compound interval corresponds to a simple interval. A compound interval can be thought of as a simple interval where one of the notes has been raised or lowered by one or more octaves. Subtracting seven from a compound interval will give you the interval number of the simple interval. For example, to determine the simple interval equivalent of a tenth you subtract seven from ten to find that the equivalent is a third. Below are several compound intervals with the corresponding simple interval shown next to each one:
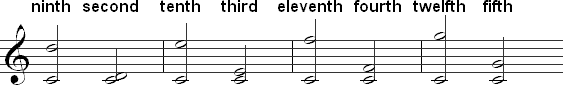
The chart below shows the interval name, the number of half steps in each intervals, and the equivalent simple interval for the most commonly used compound intervals:
| Compound intervals | Half steps | Simple interval equivalent |
|---|---|---|
| minor ninth | 13 | minor second |
| major ninth | 14 | major second |
| minor tenth | 15 | minor third |
| major tenth | 16 | major third |
| perfect eleventh | 17 | perfect fourth |
| perfect twelfth | 19 | fifth |
| minor thirteenth | 20 | minor sixth |
| major thirteenth | 21 | major sixth |
Compound intervals are important in chord construction, so it is essential that you understand the concept. Intervals of a ninth, eleventh, and thirteenth are commonly used in extended chords.
